Enigme de Sheldon “Solve this if you are a genius” #1
Une énigme facile pour commencer cette nouvelle série d’énigmes de Sheldon.
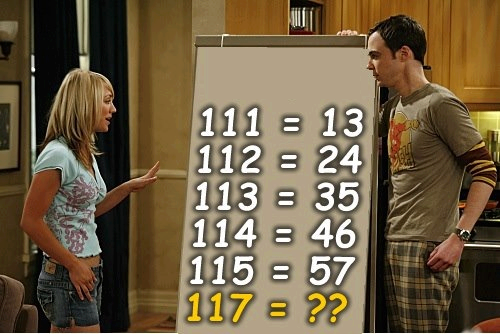
En suivant la logique (111=13, 112=24, 113=35, 114=46, 115=57), que vaut 117 ?
“Solve this if you are a genius” – Sheldon Cooper – The Big Bang Theory
Voir la solution
6th line = 6 plus 1+1+7 = 9 thus 69
en faite faut faire les calcules en 2 étapes soit : addition et multiplication :
1+1+1=3, (1×1)x1 = 1 soit le résultat 13,
1+1+2=4, (1×1)x2=2 soit le résultat 24
etc
1+1+7=9,(1×1)x7=7 donc le résultat est 79
les addition pour trouvé l’unité et la multiplication pour trouvé le chiffre des dizaines rien de bien compliqué
Sinon il y a la solution effectivement plus simple comme 77 = 11 x 7 , 77 +1+1 =79 donc 117 = 79
11=11×1, 11+1+1 = 13 donc 111=13
22=11×2, 22+1+1=24 donc 112 = 24
etc
En tout cas excellente journée, sa ma permit de me décontracté 2 minutes.
(1*1*7=7) et puis j’ajout a l’autre coté (1+1+7=9) c’est comme l’analyse matricielle
trop mais trop facile NEXT !!!
111= 13 / 112=24/ 113=35 / 114=46/ 115=57
(24-13=11)/ (35-24=11)/(46-35=11) /(57-46=11)
Si on suit cette logique donc 116= 57+11=68 alors 116=68
Enfin 117= 68+11= 79 ou tout simplement 117= ((115=57)+22)) alors mes amis 117=79
en résumé 111= 13 / 112=24/ 113=35 / 114=46/ 115=57 /”116=68″/117=79
13+11= 24+11 = 35+11 = 46+11= 57+11= 68+11=79 ou 57+22=79
68 a chaque on ajoute 11 a chq fw
Trop facile !!!
” 79 “
79
69
J’ai plutôt l’impression que le 1er chiffre du résultat correspond au produit des 3 1ers (1*1*7=7) et le second à la somme des 3 1ers (1+1+7 = 9)
@aliomer
Tombé dans le piège ! 😀
Pour faire simple : En ajoutant +1 à gauche du signe = , il faut ajouter +11 de l’autre côté.
Pour passer de 115 à 117 on ajoute +2, et donc il faut ajouter +22 de l’autre côté, soit 57 + 22 = 79.
cest pas 79 cest68
@Aymerik54
Bien Expliqué
79
J’ai pas trop compris l’explication. 😛
J’ai pris le dernier chiffre de 117 et pour trouver le second, j’ai fait la somme des chiffres donc 7 pour le premier chiffre et 1 + 1 + 7 = 9 pour le second : 79.
Ca marche. 🙂